Explicacion del tema

                     https://youtu.be/AbZO0IWSnjk

Ver más tarde          

Analisis Movimiento Rectilineo y De Caida Libre

Movimiento rectilíneo uniforme. Representación gráfica de la posición, velocidad y aceleración de un móvil en función del tiempo.

Un movimiento es rectilíneo cuando el móvil describe una trayectoria recta, y es uniforme cuando suvelocidad es constante en el tiempo, dado que su aceleración es nula. Nos referimos a él mediante el acrónimo MRU.

El MRU (movimiento rectilíneo uniforme) se caracteriza por:

• Movimiento que se realiza sobre una línea recta.
• Velocidad constante; implica magnitud y dirección constantes.
• La magnitud de la velocidad recibe el nombre de celeridad o rapidez.
• Aceleración nula
• 

• Movimiento rectilíneo uniformemente acelerado

  El movimiento rectilíneo uniformemente acelerado (MRUA), también conocido como movimiento rectilíneo uniformemente variado (MRUV), es aquel en el que un móvil se desplaza sobre una trayectoriarecta estando sometido a una aceleración constante.
  Un ejemplo de este tipo de movimiento es el de caída libre vertical, en el cual la aceleración interviniente, y considerada constante, es la que corresponde a la gravedad.
  También puede definirse el movimiento como el que realiza una partícula que partiendo del reposo es acelerada por una fuerza constante.
  El movimiento rectilíneo uniformemente acelerado (MRUA) es un caso particular del movimiento uniformemente acelerado (MUA).
• 
• 
  
• Movimiento de Caída Libre

  En física, se denomina caída libre al movimiento de un cuerpo bajo la acción exclusiva de un campo gravitatorio. Esta definición formal excluye a todas las caídas reales influenciadas en mayor o menor medida por la resistencia aerodinámica del aire, así como a cualquier otra que tenga lugar en el seno de un fluido; sin embargo es frecuente también referirse coloquialmente a éstas como caídas libres, aunque los efectos de la viscosidad del medio no sean por lo general despreciables.

  El concepto es aplicable también a objetos en movimiento vertical ascendente sometidos a la acción desaceleradora de la gravedad, como un disparo vertical; o a satélites no propulsados en órbita alrededor de la Tierra, como la propia Luna. Otros sucesos referidos también como caída libre lo constituyen las trayectorias geodésicas en el espacio-tiempo descritas en la teoría de la relatividad general.

  
  

  Ejemplos de caída libre deportiva los encontramos en actividades basadas en dejarse caer una persona a través de la atmósfera sin sustentación alar ni de paracaídas durante un cierto trayecto.

Trayectoria balística

La trayectoria balística es la trayectoria de vuelo que sigue un proyectil sometido únicamente a su propia inercia y a las fuerzas inherentes al medio en el que se desplaza, principalmente la fuerza gravitatoria.

La ciencia que estudia los fenómenos balísticos en general se denomina balística. La balistica exterior estudia la trayectoria balística bajo diversas condiciones.

Cuando sobre el proyectil tan solo actúa la gravedad, la trayectoria balística es una parábola. Sin embargo, la presencia de otras fuerzas, tales como la resistencia aerodinámica (atmósfera), la fuerza de sustentación, la fuerza de Coriolis (efecto de la rotación terrestre), etc. hace que la trayectoria real sea algo diferente de una parábola.

Algunos proyectiles autopropulsados se denominan balísticos haciendo hincapié que no existe propulsión nada más que en la fase inicial de lanzamiento ('fase caliente'). Un ejemplo de ello son los misiles balísticos que en su fase de caída carecen de autopropulsión.

Ecuaciones de la trayectoria balística

Utilizaremos las siguientes hipótesis simplificadoras:

• El alcance del proyectil es suficientemente pequeño como para poder despreciar la curvatura de la superficie terrestre (la aceleración gravitatoria ${\displaystyle \mathbf {g} \,}$ es normal a dicha superficie);
• La altura que alcanza el proyectil es suficientemente pequeña como para poder despreciar la variación del campo gravitatorio terrestre con la altura;
• La velocidad del proyectil es suficientemente pequeña como para poder despreciar la resistencia que presenta el aire a su movimiento.
• No tendremos en cuenta el efecto de rotación de la Tierra que, como veremos más adelante, tiende a desviar el proyectil hacia la derecha de su trayectoria cuando el movimiento tiene lugar en el hemisferio Norte.
• 

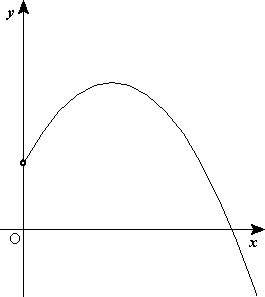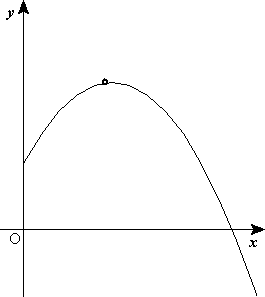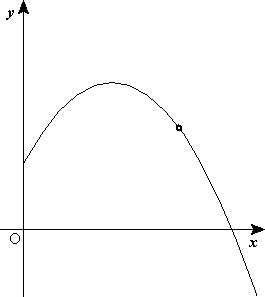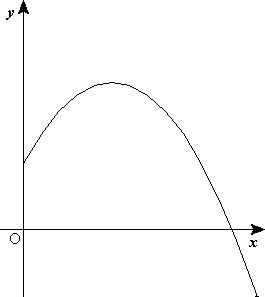
Supongamos que se dispara el proyectil con una velocidad inicial  que forma un ángulo  con la horizontal. Escogeremos el plano xy coincidiendo con el plano de la trayectoria (definido por  y ), con el eje y vertical y dirigido hacia arriba y el origen O coincidiendo con la posición de disparo del proyectil. Tenemos:

La componente horizontal de la velocidad permanece invariable, pero la componente vertical cambia en el transcurso del tiempo. En la figura 1 se observa que el vector velocidad inicial ${\displaystyle \,v_{0}}$ forma un ángulo inicial ${\displaystyle \,\theta _{0}}$ respecto al eje x; el ángulo ${\displaystyle \,\theta }$ que forma la velocidad con la horizontal, que coincide con la pendiente de la trayectoria, cambia conforme avanza el proyectil..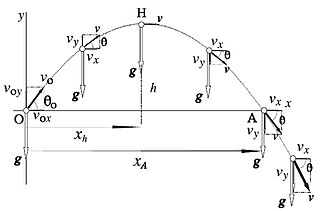

Velocidad relativa

La velocidad relativa entre dos cuerpos es el valor de la velocidad de uno de ellos tal como la mediría un observador situado en el otro. Denotaremos al valor la velocidad relativa del cuerpo B respecto al cuerpo A como .

Velocidad relativa en mecánica clásica

Dados dos observadores, A y B, cuyas velocidades medidas por un tercer observador son ${\displaystyle \mathbf {v} _{\text{A}}\,}$ y ${\displaystyle \mathbf {v} _{\text{B}}\,}$, respectivamente, la velocidad relativa de B con respecto a A se denota como ${\displaystyle \mathbf {v} _{\text{BA}}\;}$ y viene dada por:

${\displaystyle \mathbf {v} _{\text{BA}}=\mathbf {v} _{\text{B}}-\mathbf {v} _{\text{A}}}$

Naturalmente, la velocidad relativa de A con respecto a B se denota como ${\displaystyle \mathbf {v} _{\text{AB}}\;}$ y viene dada por:

${\displaystyle \mathbf {v} _{\text{AB}}=\mathbf {v} _{\text{A}}-\mathbf {v} _{\text{B}}}$

de modo que las velocidades relativas ${\displaystyle \mathbf {v} _{\text{BA}}\;}$ y ${\displaystyle \mathbf {v} _{\text{AB}}\;}$ tienen el mismo módulo pero sentidos opuestos.

El cálculo de velocidades relativas en mecánica clásica es totalmente aditivo y encaja con la intuición común sobre velocidades; de esta propiedad de la aditividad surge el método de la velocidad relativa.

Consideremos dos partículas A y B que se mueven en el espacio y sean ${\displaystyle {{\mathbf {r} }_{\text{A}}}}$ y ${\displaystyle {{\mathbf {r} }_{\text{B}}}}$ sus vectores de posición con respecto al origen O de un referencial dado. Las velocidades de A y B medidas en ese referencial son

${\displaystyle {{\mathbf {v} }_{\text{A}}}={\frac {d{{\mathbf {r} }_{\text{A}}}}{dt}}\quad \quad \quad \quad {{\mathbf {v} }_{\text{B}}}={\frac {d{{\mathbf {r} }_{\text{B}}}}{dt}}}$

Los vectores de posición de la partícula B con respecto a la A y de la A con respecto a la B están definidos por

${\displaystyle {{\mathbf {r} }_{\text{BA}}}={\overrightarrow {\text{AB}}}={{\mathbf {r} }_{\text{B}}}-{{\mathbf {r} }_{\text{A}}}\quad \quad \quad \quad {{\mathbf {r} }_{\text{AB}}}={\overrightarrow {\text{BA}}}={{\mathbf {r} }_{\text{A}}}-{{\mathbf {r} }_{\text{B}}}}$

y las velocidades de B con respecto a A y de A con respecto a B son

${\displaystyle {{\mathbf {v} }_{\text{BA}}}={\frac {d{{\mathbf {r} }_{\text{BA}}}}{dt}}\quad \quad \quad \quad {{\mathbf {v} }_{\text{AB}}}={\frac {d{{\mathbf {r} }_{\text{AB}}}}{dt}}}$

de modo que al ser ${\displaystyle {{\mathbf {r} }_{\text{BA}}}=-{{\mathbf {r} }_{\text{AB}}}}$ también resulta que ${\displaystyle {{\mathbf {v} }_{\text{BA}}}=-{{\mathbf {v} }_{\text{AB}}}}$. Esto es, las velocidades relativas de B con respecto a A y de A con respecto a B son iguales y opuestas. Efectuando las derivadas indicadas en resulta

${\displaystyle {{\mathbf {v} }_{\text{BA}}}={\frac {d{{\mathbf {r} }_{\text{BA}}}}{dt}}={\frac {d{{\mathbf {r} }_{\text{B}}}}{dt}}-{\frac {d{{\mathbf {r} }_{\text{A}}}}{dt}}={{\mathbf {v} }_{\text{B}}}-{{\mathbf {v} }_{\text{A}}}}$

${\displaystyle {{\mathbf {v} }_{\text{AB}}}={\frac {d{{\mathbf {r} }_{\text{AB}}}}{dt}}={\frac {d{{\mathbf {r} }_{\text{A}}}}{dt}}-{\frac {d{{\mathbf {r} }_{\text{B}}}}{dt}}={{\mathbf {v} }_{\text{A}}}-{{\mathbf {v} }_{\text{B}}}}$

de modo que obtendremos la velocidad relativa entre las dos partículas restando vectorialmente sus velocidades con respecto a un mismo referencial

Cinemática del sólido rígido

El concepto de velocidad relativa es particularmente útil en la cinemática del sólido rígido. Si se acepta que las distancias entre los diversos puntos de un sólido rígido no varían duranto, entonces, conocida la velocidad angular ${\displaystyle {\boldsymbol {\omega }}\,}$ del sólido en cada instante y la velocidad de un punto P del mismo, podemos conocer la velocidad de cualquier otro punto P' mediante la relación:

donde:

${\displaystyle \mathbf {v} _{\text{P}},\,\,\mathbf {v} _{\text{P'}}}$, son las velocidades de los puntos P y P' medidos en un mismo referencial considerado como fijo o absoluto.

${\displaystyle {\overrightarrow {\text{PP'}}}}$ es el vector posición del punto P' con respecto al punto P; esto es que tiene como origen el punto P y como extremo el P'. En general, este vector, aunque de módulo constante, cambiará de dirección en el espacio en el transcurso del tiempo.

caída libre aplicaciones

Ecuaciones para un cuerpo en caída libre

Bajo condiciones terrestres normales, cuando los objetos se mueven debido a una fuerza gravitacional constante, un conjunto de ecuaciones dinámicas describen las trayectorias resultantes. Por ejemplo, la ley de gravitación universal simplifica a 

F = mg, donde m es la masa del cuerpo. Esta suposición es valida para objetos que caen de la tierra de distancias relativamente cortas de experiencia diaria, pero para distancias muy largas (como la trayectoria de una nave espacial) no son muy validas. En este artículo se desprecia la resistencia del aire.

Cerca de la superficie de la tierra, use g = 9.8 m/s² (metros por segundo cuadrado) aproximadamente. Para otros planetas multiplique g por el respectivo factor de escala. Es importante usar las unidades correctas para g, d, t y v. Considerando el SI, g se medirá en metros por segundo cuadrado y d se medirá en metros, t en segundos y v en metros por segundo.

En todos los casos se asume que el cuerpo inicia en un estado de reposo (eso significa que su velocidad inicial es Cero)además, la resistencia del aire es despreciada. Generalmente, en la atmósfera de la tierra, esto es valido para caídas que no duren más de 5 segundos (tiempo en que la velocidad del objeto será un poco menor que el valor del vacío de 49m/s, debido a la resistencia del aire). Para un cuerpo que se encuentre en una atmósfera más delgada como la que se presenta cerca del nivel del mar, la velocidad límite se alcanza exponencialmente entre 8 y 15 segundos, después de que se mantenga una velocidad constante de 100 m/s en objetos compactos con densidades parecidas a las del agua y a la de los metales comunes.

A excepción de la última fórmula, estas formulas también asumen que g no varía significativamente con la altura durante la caída (Por lo cual, se asume una aceleración constante). Para situaciones donde la distancia del centro del planeta varía significativamente durante la caída que produzcan cambios significativos en el valor de g, la última ecuación debería usarse para una mayor exactitud.

Distancia d recorrida por un objeto en caída libre con tiempo t:
Tiempo t transcurrido por un objeto en una distancia de caída d:
Velocidad instantánea vi de un cuerpo en caída libre después de un tiempo elapsado t:
Velocidad instantánea vi de un cuerpo en caída libre que ha recorrido una distanciad:
Velocidad promedio va de un cuerpo que ha caído en un tiempo t:
Velocidad promedio va de un cuerpo en caída libre que ha recorrido una distancia d :

El descubrimiento de la Ley de la Gravitación Universal

Un momento culminante en la historia de la Física fue el descubrimiento realizado por Isaac Newton de la Ley de la Gravitación Universal: todos los objetos se atraen unos a otros con una fuerza directamente proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia que separa sus centros. Al someter a una sola ley matemática los fenómenos físicos más importantes del universo observable, Newton demostró que la física terrestre y la física celeste son una misma cosa. El concepto de gravitación lograba de un solo golpe:

• Revelar el significado físico de las tres leyes de Kepler sobre el movimiento planetario.
• Resolver el intrincado problema del origen de las mareas 
• Dar cuenta de la curiosa e inexplicable observación de Galileo Galilei de que el movimiento de un objeto en caída libre es independiente de su peso.
• 
  

La naturaleza cuadrático inversa de la fuerza centrípetra para el caso de órbitas circulares, puede deducirse fácilmente de la tercera ley de Kepler sobre el movimiento planetario y de la dinámica del movimiento circular uniforme:

1. Según la tercera ley de Kepler el cuadrado del periodo P es proporcional al cubo del semieje mayor de la elipse, que en el caso de la circunferencia es su propio radio r, P²=kr³.

2. La dinámica del movimiento circular uniforme, nos dice que en una trayectoria circular, la fuerza que hay que aplicar al cuerpo es igual al producto de su masa por la aceleración normal, F=mv²/r.

3. El tiempo que tarda un planeta en dar una vuelta completa es el cociente entre la longitud de la circunferencia y la velocidad, P=2p r/v.

Newton comparó la aceleración centrípeta de la Luna con la aceleración de la gravedad g=9.8 m/s². La aceleración centrípeta de la Luna es a_c=v²/r=4p ²r/P², con r=3.84·10⁸ m y P=28 días=2.36·10⁶ s, se obtiene a_c=2.72·10^-3 m/s²

EVOLUCIÓN HISTÓRICA DE LA RELACIÓN FUERZA-MOVIMIENTO

El movimiento es, sin duda, el primer aspecto del mundo físico estudiado por el hombre. Las observaciones del movimiento de los planetas y las estrellas se remontan a las antiguas civilizaciones de Egipto y Mesopotamia (ca. 3000 a.C.), siendo eminentemente prácticas, con el objetivo de elaborar calendarios. Sin embargo, serán los grandes pensadores griegos los que comiencen a desprenderse del mito y a estudiar de forma racional los fenómenos naturales.

El concepto aristotélico de movimiento

Para Aristóteles (s. IV a.C.), el estado natural de un cuerpo era el reposo. Aparte del mundo celeste donde el movimiento natural único sería el circular uniforme, en el mundo inferior (sublunar), debemos distinguir entre el movimiento rectilíneo vertical y los demás.

El movimiento vertical es un movimiento natural que viene determinado por la tendencia del elemento presente a volver a su lugar natural cuando se encuentre fuera de él. Así, cuando se calienta un vaso de agua, el vapor se eleva por la presencia del elemento fuego que tiende a llegar a la esfera de fuego. Al enfriarse, el vapor abandona el fuego, y el agua, que es ahora el elemento predominante, tiende a ocupar su lugar natural abajo. Como consecuencia, en el movimiento de caída libre de los cuerpos, la velocidad deber ser proporcional a la cantidad de su elemento constituyente, así, los cuerpos más pesados caerían más deprisa que los más ligeros.

Este pensamiento no era el resultado de experiencias mal realizadas o de errores de medidas, ya que los antiguos griegos no experimentaban, sólo especulaban, sino que era una consecuencia característica de un esquema global de pensamiento.